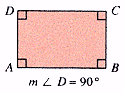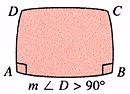Section 7.6: Mathematics, Art, and Non-Euclidean Geometries

7.6 Outline

1. Golden rectangles
   1. definition
   2. divine proportion
   3. tau
2. Mathematics and art
   1. golden ratios in art
   2. proportions of the human body
   3. spiral constructed using a golden rectangle
3. Projective geometry
   1. Duccio’s Last Supper
   2. Hogarth’s Perspective Absurdities
   3. false perspective
   4. Masaccio’s The Holy Trinity
   5. Durer’s Designer of the Lying Woman
4. Non-Euclidean geometry
   1. Euclid’s fifth postulate
   2. Saccheri quadrilateral
   3. Lobachevskian postulate
   4. hyperbolic geometry
   5. pseudosphere
   6. great circle
   7. elliptic geometry
   8. table showing comparisons of major two-dimensional geometries

7.6 Essential Ideas

A Saccheri quadrilateral has right angles as base angles and sides of equal length.

The summit angles may or may not be right angles.

The Lobachevskian Postulate: The summit angles of a Saccheri quadrilateral are acute.

This section discusses projective geometry and its relationship to three-dimensional representation in art. Next, non-Euclidean geometries are investigated with the idea in mind that Euclidean geometry is not the only possible geometry. The principle non-Euclidean geometries are hyperbolic and elliptic geometries.

A representative line in each geometry is shown in color for each models, and the shaded portion showing a Saccheri quadrilateral is shown directly below the respective models.
Geometry is on a plane:	Geometry is on a pseudosphere:	Geometry is on a sphere:
The sum of the angles of a triangle is 180 degrees. Lines are infinitely long.	The sum of the angles of a triangle is less than 180 degrees. Lines are infinitely long.	The sum of the angles of a triangle is more than 180 degrees. Lines are finite in length.

The essential idea in classifying the correct geometry is the Lobachevskian postulate:
The summit angles of a Saccheri quadrilateral are acute.